
One of the best known mathematical formulas is Pythagorean Theorem, which provides us with the relationship between the sides in a right triangle. The first of these special right triangles is the isosceles right triangle, also known as the 45-45-90 triangle because of the measures of the angles of the triangle. Since the triangle is isosceles, we know that the two legs of the triangle are the same. You can now use the Pythagorean Theorem to find the length of the hypotenuse.I recently encountered a Stack Overflow question (since closed) in which the OP was testing for whether a triangle was right by whether or not it "met" the criteria of the Pythagorean Theorem (i.e. Whether or not the square of the hypotenuse is equal to the square of the two sides).Test Review-Pythagorean Theorem & Special Right Triangles-30-60-90.
...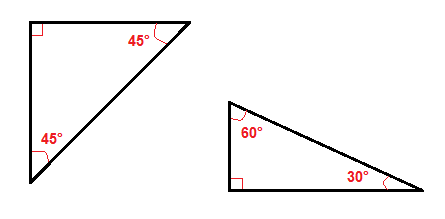
The most frequently studied right triangles, the special right triangles, are the 30, 60, 90 Triangles followed by the 45, 45, 90 triangles.The special right triangles uses the proportions between the relations of the sides and angles of a right triangle. Although all right triangles have special features trigonometric functions and the Pythagorean theorem. What students should know and be able to do at a mastery. 9.3.3.5 Know and apply properties of right triangles, including properties of 45-45-90 and 30-60-90 triangles, to solve problems and logically justify results. 9.3.3.4 Apply the Pythagorean Theorem and its converse to solve problems and logically justify results.
Another thing important to say is that the bigger the angle is, the longer the opposite side will be.Another aspect to be clear when we work with special right triangles is that the sum of the three angles will be equals to 180, but as we already know a right triangle has a 90° angle, this means that the sum of the other 2 angles will be equals to 90°, this is why when we know the value of an angle we can easily find the other angle just by subtracting the angle we know to 90°.In this triangles we are going to be using the letter “k” indicating a proportion, for example, if we have the sides “1k” and “2k”, we can see that the “2k” side is double the length of the “1k” side, so this is not the actual length of the side but it is the proportion based on the length of the other side. General properties of the trianglesA reminder before we continue, to name the sides and angles of a triangle, normally we use the letters A, B and C, where the capital letters are used to name the angles and the lowercase letters are used to name sides, where the sides are going to have the same name as the opposite angle.


 0 kommentar(er)
0 kommentar(er)
